Cement Depot Location Optimization

Introduction

The client, a prominent cement company, operates three plants located in Rajasthan, Madhya Pradesh, and Karnataka. They supply three types of cement to over 1,000 sub-districts across India. Currently, the company manages 100 depots that distribute cement to dealers via a combination of rail and road networks. However, due to recent inorganic expansion, the company is now encountering several issues including;

• High logistics costs due to sub-optimal depot locations
• Inventory management challenges, including frequent stock-outs and excess inventory at depots

To address these challenges, the company needs to optimize its supply chain and identify cost-saving opportunities. A mathematical network optimization model has been developed to determine the optimal locations for new depots, aiming to minimize logistics costs and improve overall efficiency.

Assumptions

1. Plant Distribution: Each state has one plant.
2. Cement Production: Each plant produces all three types of cement.
3. Cost of Transportation: There is a linear relationship between the distance covered and the cost of transportation.
4. Cost Consistency: The building cost for new depots and the operational cost of existing depots is approximately similar.
5. Traffic and Route Quality: Traffic flow and route quality are assumed to be similar.
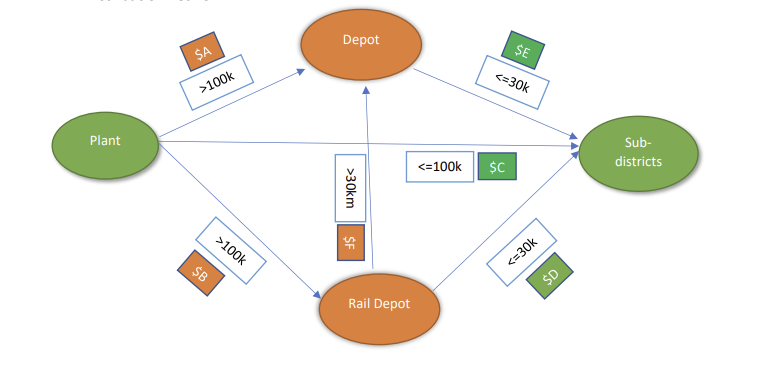
6. Distance Constraints: The table below details the distance constraints:
   • The serviceability limit of a depot is 30 km.
   • The direct dispatch radius from a plant is 100 km.
   • Cement transported from the plant to sub-districts must adhere to these distance limitations; otherwise, a penalty cost unit α is incurred for each additional kilometer.
7. Market Forces: We further assume the optimal location for a depot is influenced only by Market factors and any other influence such as varying infrastructure cost, government taxes etc. are constant across sub-districts. The diagram below illustrates this idea.

Distance Assumptions Table

From / To	Depot	Rail Depot	Sub-districts
Plant	> 100 km	> 100 km	<= 100 km
Depot	X	X	<= 30 km
Rail Depot	>= 30 km	X	<= 30 km

Distribution Network

Mathematical Formulation

To formulate the mathematical representation of the transportation costs based on your scenario, we can define the costs and distances as follows:

• plant = p
• Depot = d
• Rail Head = rh
• Sub-district = c
• Product = pd

As shown in the previous diagram we assume a specific cost when each the route is used within the distance constraints. With any extra distance covered resulting to a penalty cost. I begin by examining the scenario where all transportations are within the specified the distance limitations as case 1.

Case 1

I first examine the case where the transportation of products is well within the specific limits implying no further cost results due to distance penalties. Therefore, I sum only the specified transportation cost on each route the product used before arriving at the sub-district.

• cost of product(pd) transported = X
• cost of transport from p to d = A
• cost of transporting from p to rh = B
• cost of transporting from p to c = C
• cost of transporting from rh to c = D
• cost of transporting from d to c = E
• cost of transporting from rh to d = F

Objective function

Min (X * A _p-d + X * B _p-rh + X * C_p-c + X * D_rh-c + X * E_d-c + X * F_rh-d)

Subject to:

• At p, X_p-d + X _p-rh + X _p-c = 1
• At c, X _p-c + X _d-c + X _rh-c = 1
• At d, X _p-d+ X _p-rh + X _p-c = 0
• At rh, X _p-rh + X _rh-d+ X _rh-c = 0

Case 2

In case 2, I examine the scenario where due to demand in certain regions transportation distances of products exceed the serviceability limits thereby resulting in extra cost. In this case, I consider whether building an extra depot in this location will be cost-effective or using the existing network is more cost-efficient. The formula considers the sum of the fixed costs from operating within the distance limits plus a penalty unit cost α for every extra kilometer in distance covered multiplied by an Indicator whether a new depot is needed or not. Plus, the cost β for building a new depot multiplied by an Indicator whether a new depot is needed or not.

The binary Indicator for whether a new depot is needed is I_{β < ∑α * Pi}. Which takes a value of 1 when the cost of a new depot β is less than the sum of the penalty costs incurred due to operating in the location and 0 otherwise.

A binary indicator PI takes a value of 1 for each extra kilometer covered outside the distance limits and zero if no further kilometer is covered. The total summation \[ \sum_{n=1}^{\infty} a_n \cdot \text{PI}_n \] represents the total penalty costs.

Objective Function

MIN (Sum (fixed costs) + Sum (penalty cost * penalty indicator) * new depot indicator + (new depot cost) * new depot indicator)

Let,

• X be the cost of cement transported
• Set R represent of all possible routes from plant to sub-district
• Variable W represent the transportation cost of using a route
• β the cost of building a new depot
• α the unit penalty cost for any extra kilometer travelled

Subject to:

• ∑ (Wij)i ∈ R = Ap-d + Bp-rh + Cp-c + Drh-c + Ed-c + Frh-d , ∀i, j ∈ R
• PIn, I ∈ {0,1}
• At p, Xp-d + Xp-rh + Xp-c = 1
• At c, Xp-c + Xd-c + Xrh-c = 1
• At d, Xp-d + Xp-rh + Xp-c = 0
• At rh, Xp-rh + Xrh-d + Xrh-c = 0

How S&OP adherence can be improved

There are number of ways S&OP(Sales and Operations Planning) adherence can be improved. To help optimize business procedure. I would improve S&OP adherence by:

1. Capacity Plan Adherence

   Measuring the planned quantity of tons cement expected to move through a depot within a period vs the actual quantity that moves will be an effective measure to ensure S&OP adherence. This can be expressed as a ratio of (Planned quantity of cement – Actual quantity of cement)/ Plan quantity of cement. This ratio can help create a baseline by which future planning is estimated.

2. Percentage On-time Delivery to Sub-district

   Percentage On-time delivery is a good metric in measuring the overall efficiency of the cement supply chain. It will help track the rate of supplies that arrive to sub-districts on time. It is expressed as (planned tons expected in time t – actual tons in time t)/ planned tons expected in time t. This ratio measured within specified windows provided a good measure for our S&OP adherence.

3. Production Plan Adherence

   Measuring how well production is able to meet plan output is key to maintain tight delivery windows. This can be expressed as a ratio of (planned production – actual production)/ planned production. This can help create a baseline by which we measure future output to ensure S&OP adherence.